Basis of the further study on language – Potential
Basis of the further study on language – Potential
Floer Homology Language
TANAKA Akio
Note1
Potential of Language
¶ Prerequisite conditions
Note 6 Homology structure of Word
1
(Definition)
(Gromov-Witten potential) 
2
(Theorem)
(Witten-Dijkggraaf-Verlinde-Verlinde equation) 
3
(Theorem)
(Structure of Frobenius manifold)
Symplectic manifold (M, wM)
Poincaré duality < . , . >
Product <V1 V2, V3> = V1V2V3( 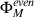 )
)
(M, wM) has structure of Frobenius manifold over convergent domain of Gromov-Witten potential.
4
(Theorem)
Mk,β (Q1, …, Qk) = 
N(β) expresses Gromov-Witten potential.
[Image]
When Mk,β (Q1, …, Qk) is identified with language, language has potential N(β).
[Reference]
Quantum Theory for language / Synopsis / Tokyo January 15, 2004
First designed on
Tokyo April 29, 2009
Newly planned on further visibility
Tokyo June 16, 2009
Sekinan Research Field of Language
[Note, 31 March 2015]
This paper was first designed for energy of language. But at that time, I could not write
the proper approach from the concept of energy by mathematical process. So I wrote
the paper through the concept of potential. Probably energy is one of the most fundamental
factors on language.
In 2003 I wrote Quantum Theory for Language , before which I wrote the manuscript focusing
the concept of quantum abstracted from the ideogram of classical Chinese written language.
The last target of manuscript was energy and meaning of quantum that was the ultimate
unit of language.
Refer to the next.
Manuscript of Quantum Theory for Language. Hakuba, Nagano. March 2003
Read more: https://srfl-paper.webnode.com/news/basis-of-the-further-study-on-language-potential/
