Floer Homology Language Note1 Potential of Language

Floer Homology Language

TANAKA Akio 

Note1 
Potential of Language
 
 
 
¶ Prerequisite conditions 
Note 6 Homology structure of Word
 
 
1 
(Definition) 
(Gromov-Witten potential)   2 
(Theorem) 
(Witten-Dijkggraaf-Verlinde-Verlinde equation)    
3 
(Theorem) 
(Structure of Frobenius manifold) 
Symplectic manifold     (M, wM) 
Poincaré duality     < . , . > 
Product     <V1°V2, V3> = V1V2V3( 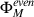) (M, wM) has structure of Frobenius manifold over convergent domain of Gromov-Witten potential.  
4 
(Theorem) 
Mk,β (Q1, ..., Qk) = 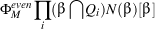  N(β) expresses Gromov-Witten potential. 
 
 
 
[Image] 
When Mk,β (Q1, ..., Qk) is identified with language, language has potential N(β). 
 
 
    

[Reference]

Quantum Theory for language / Synopsis / Tokyo January 15, 2004 

First designed on <energy of language> at 
Tokyo April 29, 2009 
Newly planned on further visibility at 
Tokyo June 16, 2009 

Sekinan Research Field of language

Back to sekinanlogoshome